Was ist überhaupt ein ARIMA-Modell?

Das ARIMA-Modell ist ein statistisches Modell, das zur Vorhersage von Zeitreihen verwendet wird. Es besteht aus drei Elementen: AutoRegressive (AR), Integrated (I) und Moving Average (MA). Der AR-Teil zeigt die Beziehung zwischen aktuellen Zeitreihenwerten und früheren Werten, der I-Teil beschreibt die Verarbeitung nicht-stationärer Prozesse und der MA-Teil zeigt die Abhängigkeit aktueller Werte von unvorhersehbaren Ereignissen in der Vergangenheit. Anhand eines vereinfachten Beispieles werde ich in diesem Post demonstrieren, wie man solch eine Analyse in R durchführt

1. Importieren der benötigten Modelle

Für das Aufstellen eines ARIMA-Modells benötigen wir folgende R-Packages:

library(dplyr)
library(forecast)
library(tseries)
library(readxl)
library(ggplot2)
library(ggthemes)

Solltest Du folgende Fehlermeldung bekommen:

in library(XXXX) : es gibt kein Paket namens ‘XXXX’

Kannst Du hiermit das fehlende Package installieren:

install.packages("XXXX")

2. Laden des Datensatzes

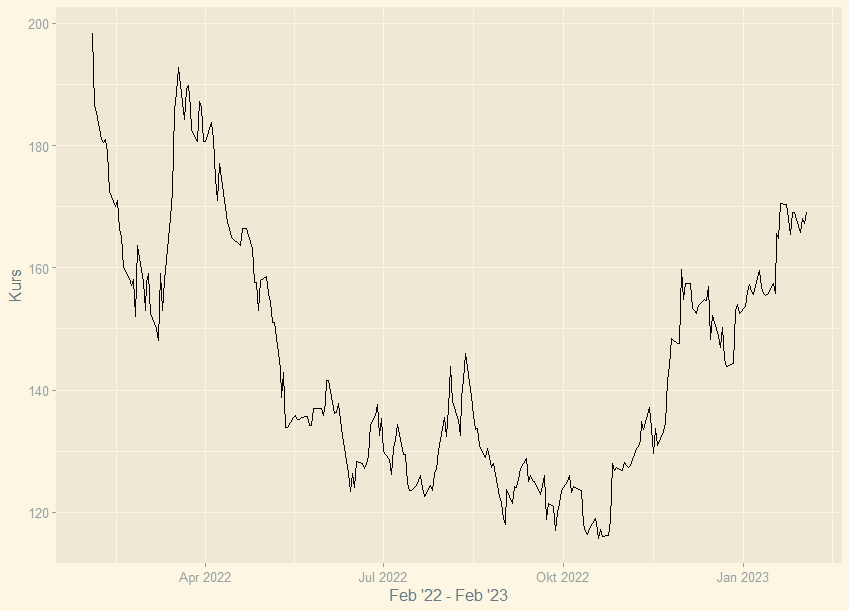
Als Beispiel-Daten benutzen wir die Aktienkurse vom 02.02.2022 - 02.02.2023 der NEW WORK SE. Die Aktienkurs-Daten kann man sich ganz einfach auf https://de.finance.yahoo.com/ beschaffen und anschließend in R importieren.

nwse <- read_excel("NWSE.xlsx", sheet = 1)
nwse$Date <- as.Date(nwse$Date, format = "%Y-%m-%d") # Datumsformatierung in YYYY-MM-DD
colnames(nwse)[6] <- "Kurs" # Adjusted Close wird in "Kurs" umbenannt
View(nwse)

Anmerkung

data: Die .csv von Yahoo-Finance sollte mit dem Legacy Editor in Excel bearbeitet und in eine .xlsx konvertiert werden um reibungslos in R damit zu arbeiten.

3. Visualisierung des Datensatzes

Um einen anfänglichen Überblick über die Daten zu bekommen, sollten diese visualiert werden. In R ist das sehr simpel und schnell gemacht mit Hilfe der Packages “ggplot2” und “ggthemes”.

chart_kurs <-ggplot(nwse, aes(x = Date, y = Kurs))+ 
  geom_line()+
  scale_x_date("Feb '22 - Feb '23")+
  ylab("Kurs")+
  theme_solarized_2()

chart_kurs

4. Prüfung auf Stationärität

Um ein ARIMA-Modell aufstelllen zu können muss überprüft werden, ob die Zeitreihe stationär ist. Stationarität bedeutet, dass statistische Eigenschaften wie der Mittelwert und Varianz zeitunabhängig sind. Sollte die zeitreihe nicht “bereinigt” von Trends sein, kann keine sinvolle Vorhersage getroffen werden, da Scheinkorrelationen bestehen.

Wir überprüfen die Zeitreihe auf Stationärität anhand des Augmented Dickey-Fuller Test (ADF-Test).

Nullhypthose (H0): Zeitreihe ist nicht stationär

Bei einem p-Wert > 0,05 wird die Nullhypothese verworfen

Output

data: nwse$Kurs
Dickey-Fuller = -1.4565, Lag order = 6, p-value = 0.8047
alternative hypothesis: stationary

5. Differenzierung

Noch liegt der p-Wert weit über 0,05, heißt die Zeitreihe ist unstationär. Um die Zeitreihe stationär zu machen, wird Differenziert um sie von Trends und dadurch entstehenden Scheinkorrelationen zu bereinigen.
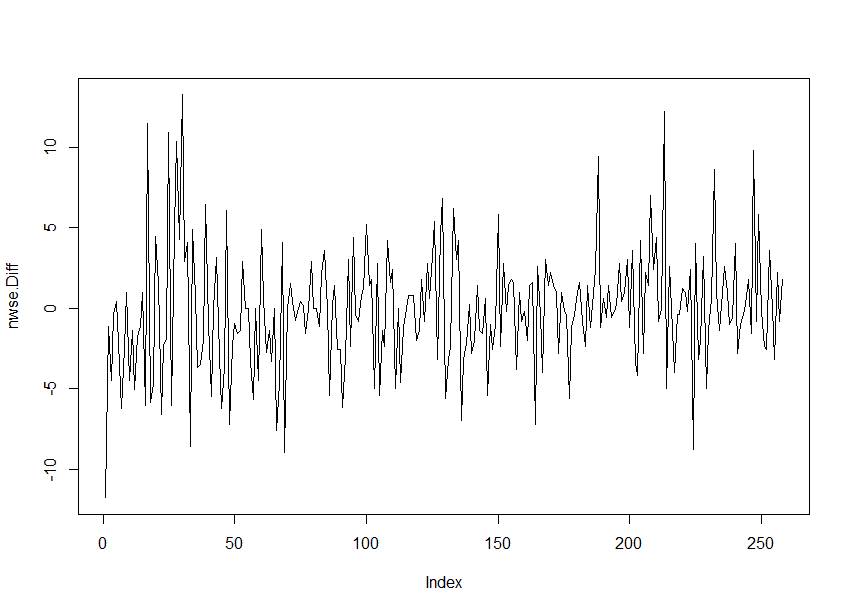
Wenn wir diese differenzierte Zeitreihe plotten, ist nicht mehr der absolute Kurswert abgebildet. Was jedoch hier zu sehen ist die Veränderung bzw. die Entwicklung des Aktienkurses im Verhältnis zu einem Zeitpunkt, beispielsweise zum Vortag. So kann man Trends und Muster in den Kursbewegungen erkennen und die Auswirkungen von Ereignissen oder Nachrichten auf den Kurs beurteilen.

nwse.Diff <- nwse$Kurs[-1] - head(nwse$Kurs,-1)
plot(nwse.Diff, type = "l")
adf.test(nwse.Diff)

Output

data: nwse.Diff
Dickey-Fuller = -6.0359, Lag order = 6, p-value = 0.01
alternative hypothesis: stationary

6. Bestimmung der ARIMA-Notation

Für das Arima Modell müssen noch die richtigen Parameter bestimmt werden.

Die allgemeine ARIMA Notation: 𝐴𝑅𝐼𝑀𝐴(𝑝, 𝑑, 𝑞)

• 𝑝 = Anzahl an autoregressiven Parametern (Werten) im Modell, d. h. die Anzahl an Lags
• 𝑑 = Anzahl an aufgespaltenen Serien, d. h. die Anzahl an Differenzierungen zur Herstellung
von Stationarität
• 𝑞 = Anzahl an gleitenden Fehler-Mittelwerten

Die Parameter p und q lassen sich mit dem ACF (Autokorrelationsfunktion) und dem PACF (Partielle Autokorrelationsfunktion) bestimmen.

Der ACF zeigt die Korrelation einer Größe mit sich selbst zu einem früheren Zeitpunkt.

Der PACF zeigt ebefalls die Korrelation einer Größe mit sich selbst zu einem früheren Zeitpunkt, jedoch sind Auswirkungen von früheren Zeitpunkten bereits berücksichtigt.

acf(nwse.Diff)
pacf(nwse.Diff)

7. Aufstellung des ARIMA-Modells

Mit der Funktion auto.arima() lassen sich die ARIMA Parameter automatisiert bestimmen und man kann ein gefittetes Modell aufstellen.

fit_model <- auto.arima(nwse.Diff)
summary(fit_model)

Output

Series: nwse.Diff<br> ARIMA(1,1,2) 

8. Vorhersage

Mit der forecast() Funktion lässt sich eine Vorhersage für die nächste Periode anhand des fitted Modell treffen.

h steht hier in diesem Fall für die Periode. Da die Zeitreihe aus Tagen besteht, entspricht h=1 einem Tag.

fc <- forecast(fit_model, h = 1)
fc
plot(fc)

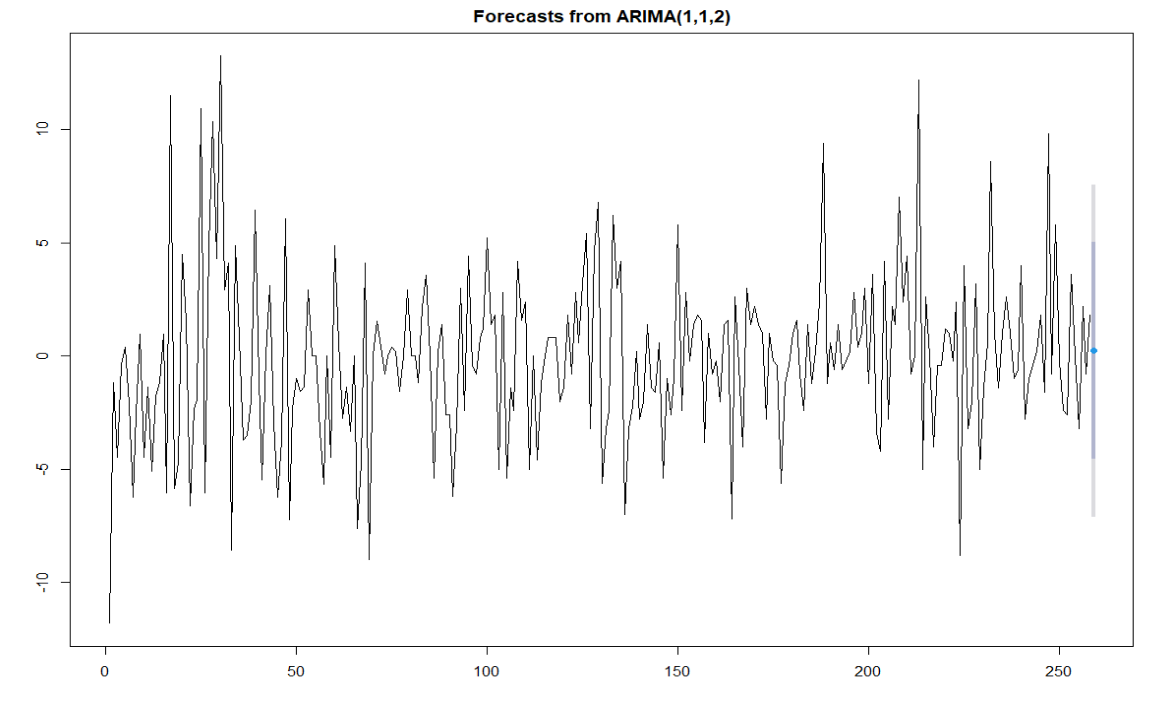
Diese Funktion gibt Konfidenzintervall von 80% aus. Die Vorhersage liegt im Intervall zwischen 164.4404 und 174.0207. Heißt, der Aktienkurs wird am nächsten Tag mit 80%iger Wahrscheinlichkeit zwischen diesen beiden Werten liegen.

Dies ist ebenfalls noch mal im Plot abgebildetet. Der dunkelblau gefärbte Teil stellt das 80% Intervall und der hellblaue das 95% Intervall dar.